
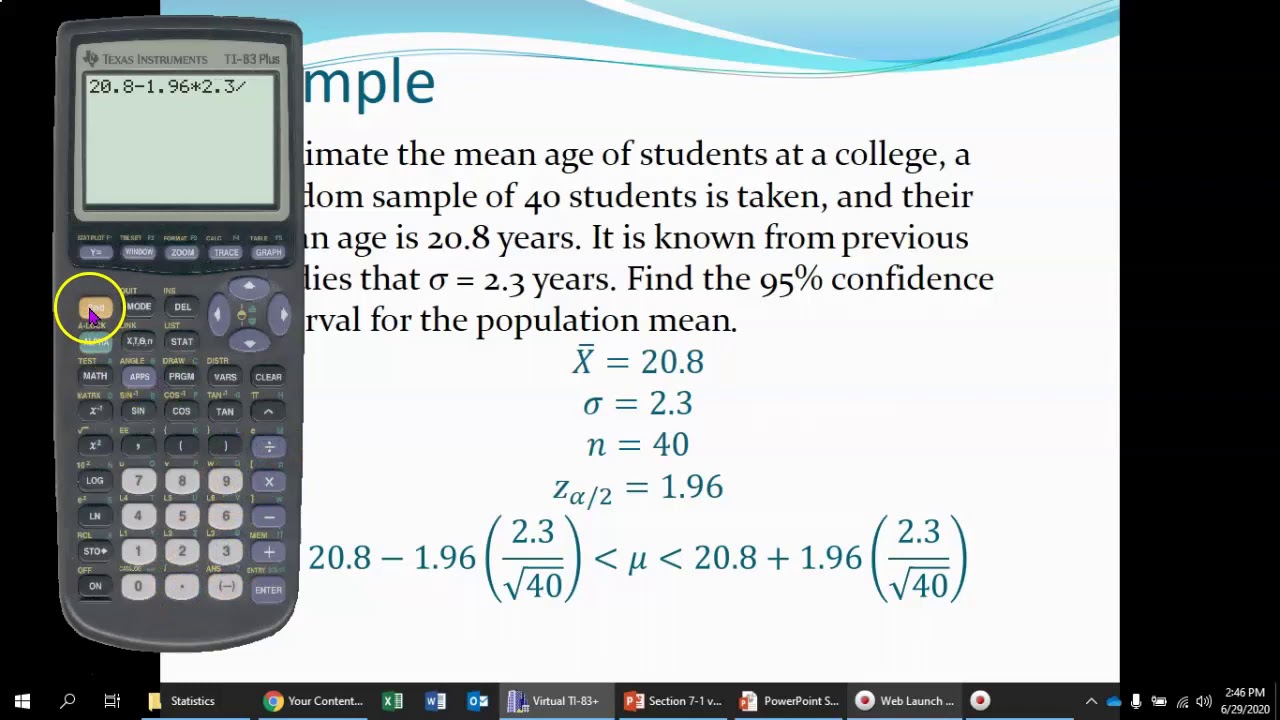
We might be more accurate if we were to say that the mean µ is somewhere between two values. Introduction to Confidence Intervals 9.12 In this class, and in many applications of statistics, the sample standard deviation sx is used as the point estimate for the population standard deviation σ. In more advanced statistics classes concern over bias in the sample standard deviation as an estimator for the population standard deviation is considered more carefully. The sample standard deviation sx is a reasonable point estimate for the population standard deviation σ. Point estimate for the population standard deviation σ Is x really the exact value of µ for all the males at the national campus? No, the sample mean is not going to be the same as the true population mean. That would make the error equal to √( x − x) 2 = zero. We do not know µ! So we say x is a point estimate for µ. Unfortunately, the whole reason we were using the sample mean x to estimate the population mean µ is because we did not know the population mean µ.įor example, given the mean body fat index (BFI) of 51 male students at the national campus is x = 19.9 with a sample standard deviation of sx = 7.7, what is the error |( x - µ )| if µ is the average BFI for male COMFSM students?
Note that the error of an estimate is the distance of the statistic from the parameter. Note that to take a positive value we need to use either the absolute value |( x - µ )| or √( x - µ ) 2. The error of a point estimate is the magnitude of estimate minus the actual parameter (where the magnitude is always positive). The sample mean x for a random sample will not be the exact same value as the true population mean µ. The sample mean x is a point estimate for the population mean µ Point Estimate for the population mean µ and Error The normal distribution of sample means for many samples taken from a population provides a mathematical way to calculate a range in which we expect to "capture" the population mean and to state the level of confidence we have in that range's ability to capture the population mean µ. The statistic we will focus on is the sample mean x. There are special circumstances under which a sample mode and median might be a good estimate of a population mode and median, these circumstances are not covered in this class. The population mode and median usually cannot be inferred from a smaller random sample. Populations are more likely to have single outliers than a smaller random sample. The population minimum, maximum, and range cannot be inferred from the sample minimum, maximum, and range.

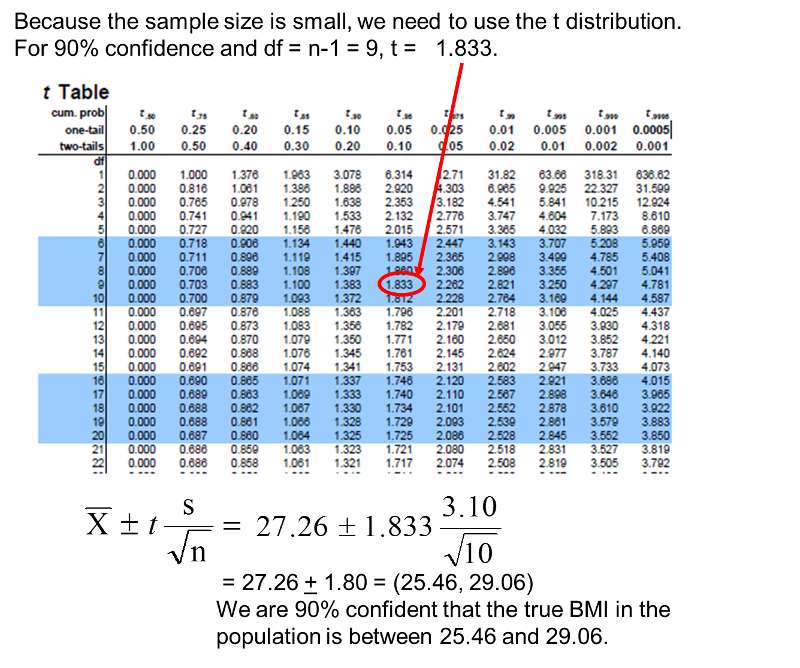
The population size N cannot be inferred from the sample size n. Some population parameters cannot be inferred from the statistic. When we use a statistic to estimate a parameter, the verb used is "to infer." We infer the population parameter from the sample statistic. Whenever we use a single statistic to estimate a parameter we refer to the estimate as a point estimate for that parameter. I think it is A) Normal distribution as the sampling distribution of the sample mean approaches u for large sample sizes.however n=66 doesnt really seem like a 'large' sample size to me so Im not sure about this.Īctually Ive just noticed that the questions gives the SAMLPLE standard deviation.9.12 Introduction to confidence intervals for the meanĩ.18 Inferences and confidence intervals for n > 30 where σ is knownĩ.2 Confidence intervals for n > 5 using sxĩ.4 Deciding on a sample size Inference and Point Estimates 9.1 I am unsure of whether the assumption I must make is A) Normal distribution or C) Any distribution. I add an subtract this to the sample mean to get the bounds for a 99% C.I.Īnd I get 2.8963 and 5.2237. I then multiply this value by (std deviation)/sqrt(sample size) => so 2.756*3.67/sqrt(66).Īnd this gives me 1.1637. What is the assumption you must make regarding this population distribution?Ī) Normal B) t distribution C) Any distributionįor a 99% interval I take the value of z from the z tables where the probability is 0.005 (as 2 * 0.005 = 1%), which is 2.756. Construct a confidence interval of 99% for the true average number of hour spent studying in a week.


 0 kommentar(er)
0 kommentar(er)
